 |
Sujet : Contexte : Date : Auteur : |
Courbes de Bézier En hommage à l'ingénieur 1999 Cédric BRAY |
 |
Sujet : Contexte : Date : Auteur : |
Courbes de Bézier En hommage à l'ingénieur 1999 Cédric BRAY |
L'informaticien qui ne connaît pas les courbes de Bézier obtient des objets en 3 dimensions dont les contours sont grossièrement approximés à des segments (sauf s'il emploie de longs détours mathématiques.)
Relativement à ce problème, les courbes de Bézier sont un outil formidable : à partir de 2 points et de leurs tangentes, il est possible de construire une portion de courbe douce entre ces points ; finies les sphères aux allures de boules à facettes!
Une courbe de Bézier dépend de points particuliers appelés points de contrôle. La donnée de ces points de contrôle (ordonnés) détermine parfaitement un tracé.
Le nombre minimal de points de contrôle nécessaire à la construction d'une courbe de Bézier est 3 (courbe quadratique).
Partons donc de 3 points du plan A, B, C, et prenons les milieux de 2 des côtés du triangle qu'ils définissent : soient I et J les milieux respectifs de [AB] et [BC].
Soit K le milieu de[IJ].
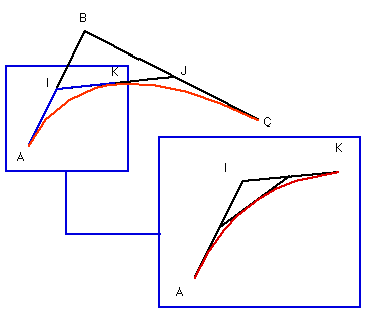
[AIK] et [KJB] sont 2 nouveaux triplets à partir desquels on peut effectuer la même procédure qu'avec A, B et C.
Au bout d'un certain nombre d'itérations, il en résulte une courbe située dans l'enveloppe convexe des points A, B, C et tangente aux droites (AB) et (BC).
Il est facile d'étendre ce procédé à un nombre quelconque de points de contrôle : la fonction qui permet de construire une courbe de Bézier à partir d'un nombre n fixé de points de contrôle s'applique récursivement aux 2 n-uplets de points obtenus après chaque étape de construction en cascade des milieux.
Quatre points peuvent servir à définir 2 vecteurs tangents à 2 points d'une courbe. L'inconvénient réside dans le fait que la norme de ces vecteurs tangents, ainsi que le sens (ce qui peut toutefois s'avérer utile...), déterminent la forme finale de la courbe.
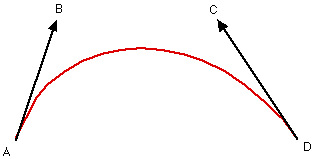
Ayant les 2 extrémités de notre courbe, on construit donc à l'aide des tangentes connues en ces points les 2 autres points de contrôle intermédiaires.
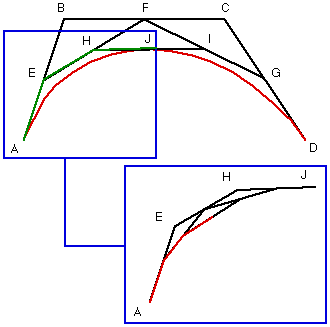
Soit E, F et G les milieux respectifs de [AB], [BC] et [CD].
Soit H et I les milieux respectifs de [EF] et [FG].
Soit J le milieu de [HI].
AEHJ et JIGD apparaissent comme deux nouveaux triplets de segments auxquels on applique le même découpage que pour ABCD.
Il est courant d'approximer une surface quelconque à une surface polyédrique.
Supposons qu'on connaisse les normales aux sommets de chaque polygone (moyennes des normales de tous les polygones adjacents).
Il s'agit d'obtenir, aux extrémités de chaque arête de chaque polygone, les vecteurs tangents qui permettront de remplacer l'affreux segment par une jolie courbe de Bézier.
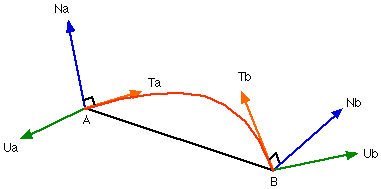
Soit le segment [AB], Na et Nb les normales en A et en B.
Soit Ua = AB ^ Na
Soit Ub = BA ^ Nb
Alors les vecteurs tangents nécessaires à la construction de la courbe de Bézier d'extrémités A et B sont :
Ta = Na ^ Ua et Tb = Nb ^ Ub
Il ne reste qu'à pondérer savamment la norme de ces vecteurs pour éviter les effets de gonflement...