Sujet : Contexte : Date : Auteur :

Triangulation de Delaunay TIPE Cartographie 3D 1999 Cédric BRAY

Problème posé

Il s'agit, à partir d'un semis de points du plan, d'obtenir un recouvrement de l'enveloppe convexe de ce semis à l'aide de triangles qui ne se chevauchent pas.

La triangulation de Delaunay fournit pour ce problème (du moins dans le cadre restreint précisé plus bas) une solution unique.

Le critère de Delaunay

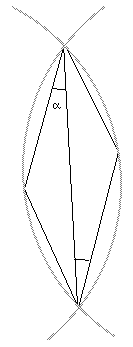
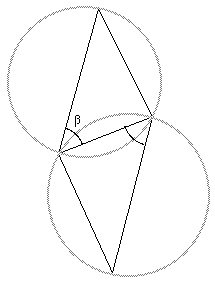
Configuration 1: Non	Configuration 2: Oui

Le critère de Delaunay , qui permet de construire la triangulation du même nom, se décline sous la forme de 2 règles équivalentes :

• Règle des cercles circonscrits :
  Aucun des cercles circonscrits aux triangles ne doit contenir d'autre point du semis.
• Règle de l'angle minimal :
  Considérons 4 points. On peut trianguler le quadrilatère convexe dont ils sont les sommets de deux façons, selon la diagonale choisie.
  Repérons, pour chaque configuration, l'angle minimal.
  Le critère de Delaunay correspond à la configuration pour laquelle cet angle est le plus grand.

Algorithme de Tsai

Cet algorithme, facile à mettre en oeuvre, exploite la règle des cercles circonscrits.
Il est récursif : on ajoute un point à une surface déjà triangulée, la triangulation initiale étant celle de l'enveloppe convexe du semis.

L'algorithme de triangulation de l'enveloppe convexe n'est pas exposé ici.
De plus, connaître initialement cette enveloppe suppose qu'on dispose par avance de tous les points, ou qu'on soit sûr qu'aucun des points à insérer ne tombera hors du cadre de base.

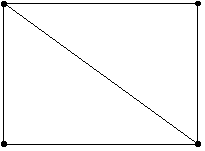
	Etudions le cas simple où l'enveloppe convexe du semis de points est un rectangle. On triangule en faisant intervenir une diagonale : le critère de Delaunay est bien vérifié.
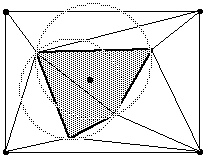
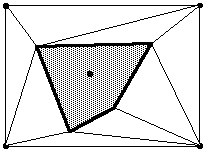
	L'algorithme de Tsai étant récusif, plaçons-nous dans l'état où la triangulation de Delaunay est déjà réalisée pour N points et examinons l'introduction d'un N+1 ème point. On commence par sélectionner les triangles dont le cercle circonscrit contient le nouveau point. Les autres triangles resteront intacts, car le critère des cercles circonscrits est bien vérifié pour l'ensemble de leurs sommets (par hypothèse) et pour le nouveau point à insérer (ils n'ont pas été sélectionnés).
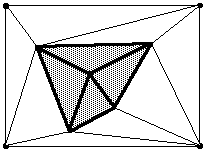
	Les triangles sélectionnés (i.e. les mauvais) formant un ensemble connexe, on élimine les arêtes qui leur sont communes pour faire apparaître un polygone contenant le point à insérer.
	Il ne reste qu'à relier les sommets du polygone précédemment mis en évidence au point à insérer : les triangles ainsi créés respectent le critère de Delaunay pour ce point (car il est un de leurs sommets), et pour tous les autres points (sinon c'est que la sélection des mauvais triangles a été mal faite).

Applications

L'avantage de cette méthode est l'automatisation totale.
Imaginons le cas d'un programme qui vise à découper une carte en parcelles triangulaires. Il suffit de fournir des points sur la carte et l'algorithme de Tsai se charge du reste.
De plus, les triangles obtenus ont la particularité d'être assez massifs, entendons par là pas trop effilés, ce qui optimise des traitements ultérieurs, comme une rastérisation par exemple.