Sujet : Contexte : Date : Auteur :

Objets à homothétie interne Pour le plaisir... 1998 Cédric BRAY

Principe

Il s'agit de découper un objet géométrique et de le reporter par homothétie dans chaque partie issue de ce découpage. On obtient ainsi récursivement des objets qui se contiennent ex-mêmes.
D'un point de vue algorithmique, on pratique une descente récursive dans l'objet ; pour l'arrêt, on précise auparavant l'ordre de l'itéré à obtenir, ou on exploite un critère graphique ( ex : ne plus découper un segment si ses extrémités sont à moins de 3 pixels d'écart.)

Par exemple, plaçons-nous en dimension 2 et pratiquons l'homothétie interne sur une ligne brisée.

Le Flocon de Von Koch.

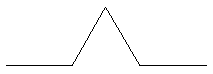
Une manière de construire le Flocon de Von Koch est d'utiliser l'exemple précédént avec le motif suivant, que l'on place sur chaque arête d'un triangle équilatéral.

Les Tamis de Sierpinski.

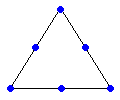
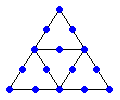
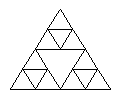
On obtient un tamis de Sierpinski en appliquant l'homothétie interne récursive à une surface.

A partir d'un triangle.

Motif de base	1ère itération	2ème itération	4ème itération

A partir d'un carré.

Motif de base	1ère itération	n-ième itération

Extension à l'espace

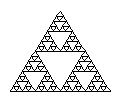
Il est facile d'étendre à l'espace ces procédés. On obtient à chaque fois un objet creux, éponge mathématique, qui est à strictement parler un des éléments d'une suite convergeant vers un objet de volume nul.
Rien que pour provoquer l'ordinateur, il peut être amusant de pousser autant que possible l'indice de récursivité : la programmation donne des objets complexes (quoique basés sur un principe simple), difficilement réalisables et manipulables avec les outils de modélisation 3D.

A partir d'un tétraèdre, à l'ordre 3	A partir d'un cube, à l'ordre 2